lkpfinder.blogg.se - Fdtd open source

I started by implementing one-dimensional FDTD to get a feel for the structure of the algorithm. So the simple version of the update equation becomes:Ĭurl_h = (hz - hz - hy + hy) We'll assume non-magnetic materials ($ \mathbf$$ John Schneider's Understanding the Finite-Difference Time-Domain Method.Dennis Sullivan's Electromagnetic Simulation Using the FDTD Method.

The two references which I found most helpful (and used significantly in this work are):

(commercial) COMSOL uses their own FDTD-like solver.

(open) Electromagnetic Template Library.

The course includes programming TLDER () and develops to different codes to analyze a microstrip transmission line (unbalanced line) and a differential pair (balanced line). There are a number of both commercial and open-source FDTD solvers: By the end, you will have developed a fully functional program that that can analyze both balanced and unbalanced transmission lines. the standard C⁄C++ language will be available in public as an open source. FDTD is now largely used to study and simulate things like sensitive RF circuits, scattering problems, and metamaterials. The FDTD method has been one of the most popular numerical tools in the.

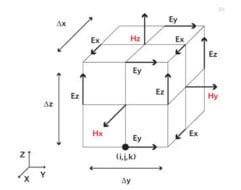
The most commonly used FDTD algorithm dates back to 1966 when Kane Yee came up with an efficient and more-accurate formulation for Maxwell's equations in a 3D lattice: Yee's Paper (1966). The Finite Difference Time Domain (FDTD) method for solving elecromagnetic fields is well studied and quite well understood. Therefore, new modeling techniques are required to design and characterize these structures. Because the structures are inherently three-dimensional, they're not well suited to being designed and modeled in the traditional ways (which, much of the time, assumes relatively planar assemblies. My research involves assembling micro-electronics from pressfit parts. Can a simple and efficient simulation/modeling software be written for electronic digital materials?